자본시장선
고려사항: 여러가지 금융상품 중에서 투자 목적의 금융상품
투자목적: 미래에 더 큰 현금흐름을 얻기 위해 현재 주어진 자금을 운용하는 것
- 위험성, 수익성 → 높은 수익성 = 높은 위험성
⇒ 수익성과 위험성을 동시에 고려해서 최적화된 투자 선택을 해야 함
Q: 수익성과 위험성을 기준으로 두고, 여기서 자본시장선이라고 하는 것을 수익성, 위험성을 가지고 있는 자산이 있을 때, 어떻게 합리적인 선택을 할 수 있을까?
[자본시장선]
정의: 무위험자산 포함 시 가장 효율적인 포트폴리오 기회 집합 (영어로는 CML)
공식: E(rp) = ((E(rm) - rf) / σm) σp + rf

리스크 프리미엄(Risk Premium)
: 위험에 대한 프리미엄 즉, 위험에 대한 대가 혹은 보상. 어떠한 투자 대상에 투자를 하는데 그 투자대상이 위험성이 있다면 그 위험성에 대한 어떤 보상을 요구할 수 있는 것.
무위험 수익률 $r_f$: 위험이 전혀 없는 자산에 투자했을 때 얻을 수 있는 수익률.

이때, 어떤 위험을 무릅쓰고 어떤 자산에 투자하여 수익률을 기대하고 있는데, 이것이 r_f보다 작다면 이 위험자산에 투자할 사람은 없음. 기대수익률과 r_f의 차이만큼 어떤 일정한 양수값을 가지는데 이것을 리스크 프리미엄이라고 정의. 기대수익률이 높으면 높을수록, 즉 r_f보다 훨씬 커서 그 차이가 크면 클수록 리스크 프리미엄은 커지는 것.
## $\cfrac{E(r_m) - r_f}{σ_m}$→ 리스크 프리미엄 → 수익성의 지표
→ 수익률의 표준편차 → 위험성의 지표
**⇒ 리스크 프리미엄을 동일한 포트폴리오가 갖는 수익률의 표준편차로 나눔**
결국 리스크 프리미엄이라는 어떤 수익성, $r_f$보다 얼마나 그 기대수익률이 큰지를 위험의 크기로 나누어주었기 때문에, 위험성으로 수익성을 표준화시킨 것으로 생각해볼 수 있음.
따라서 이 지표(계수) 하나에 수익성에 관한 것과 위험성에 관한 것이 동시에 들어가 있음. 이 표준화된 지표로서의 의미가 바로 자본시장선의 기울기, 그 계수의 의미라고 생각해볼 수 있음. 또한 위험을 나타내는 표준편차로 나누어주었기 때문에 위험의 한 단위당 시장가격, 프리미엄을 가격 보상으로 한다면 위험의 한 단위당 얼마의 가격을 매겨줄 것인지를 살펴볼 수 있는 의미라고도 볼 수 있음.

나아가 어떤 최적화된 선택에서의 균형의 원리라고 할 수 있는데, 시장 포트폴리오 대신에 임의의 p라고 하는 포트폴리오를 선택할 때, 그 포트폴리오에서 얻는 편익(benefit)이 바로 리스크 프리미엄. 그리고 그 포트폴리오를 선택했을 때 내가 부담(cost)해야 될 것이 위험($σ_p$ ).
대출 포트폴리오, 차입 포트폴리오
무위험 수익률 $r_f$에서 효율적 프론티어로의 접선을 CML, 그 접점을 시장 포트폴리오 M.
시장 포트폴리오 M을 중심으로 CML을 나누면 $r_f$와 M을 잇는 영역을 대출 포트폴리오, M을 넘어선 영역을 차입 포트폴리오 라고 함.
- 대출 포트폴리오
- 무위험자산 $r_f$와 시장 포트폴리오 M을 일정한 배분 비중으로 분산투자한 포트폴리오. 무위험자산에 투자한다는 것은 위험이 없는 자산에 투자했다는 것이기 때문에, 돈을 빌려줬다는 의미. $w_f + w_m = 1$
- 차입 포트폴리오
- M을 넘어서는 영역에서의 $w_f$는 오히려 0보다 작은 값. $w_f$에 마이너스로 투자했다는 것은 반대로 차입한 것을 의미함. 무위험 이자율로 내가 받는 것이 아니라 오히려 그것으로 대가를 주고 돈을 빌려서 시장 포트폴리오에 더 많이 투자한 것. $w_m > 1, w_f < 0$
자본 시장선의 적용
수학적으로 도출한 자본 시장선을 어떤 위험자산, 또는 위험자산과 무위험자산의 임의의 포트폴리오에 대해서, 이 자산에 내가 투자하는 것이 적정한가, 적정하지 않은가를 판단하기 위한 기준으로 사용 가능.
위 예제에서 다음과 같이 CML을 구할 수 있다.
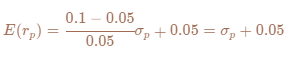
이때, 포트폴리오 p의 위험 $σ_p = 12.5%$ 를 대입해 보면 $E(r_p) = 0.175$ 가 된다.
리스크 프리미엄을 감안했을 때의 기대수익률은 0.175가 되어야하는데, 포트폴리오 p는 더 낮은 15% 밖에 안 준다는 것이므로 비효율적인 자산(포트폴리오).
이와 같이, 어떤 포트폴리오, 어떤 임의의 자산에 대해서도 자본 시장선의 공식을 적용해서 그것이 정말 적정한 투자 대상인지를 판단하는데 활용할 수가 있음.
'가치를 창출하는 데이터 분석 > 금융 데이터 분석 (금융학회)' 카테고리의 다른 글
| [Financial Data] 금융경제학 Basic #25 증권시장선의 도출 (0) | 2023.10.27 |
|---|---|
| [Financial Data] 금융경제학 Basic #24 시장모형 (0) | 2023.10.26 |
| [Financial Data] 금융경제학 Basic #22 시장 포트폴리오 (0) | 2023.10.24 |
| [Financial Data] 금융경제학 Basic #21 무위험자산을 위한 포트폴리오 (0) | 2023.10.24 |
| [Financial Data] 금융경제학 Basic #20 분산 투자의 원리와 포트폴리오 (0) | 2023.10.24 |



