분산 투자의 원리와 포트폴리오
- [예] 환율 변동에 따른 위험이 다른 세 자산
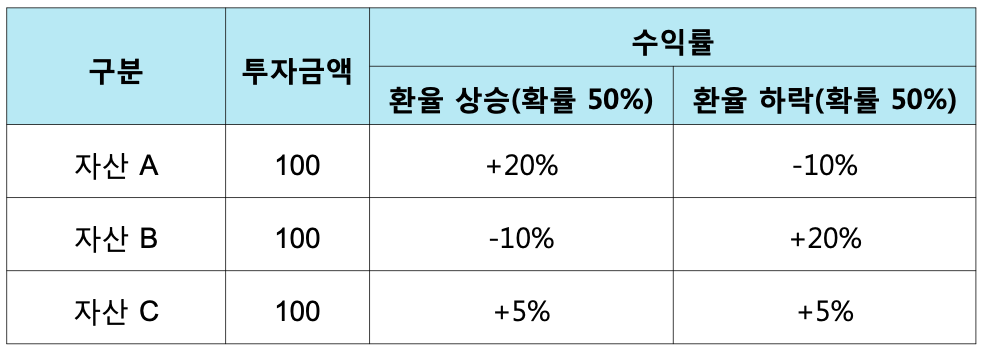
(* [7장] 분산투자의 원리: 위험자산인 주식을 투자하는 경우 수익률의 변화 방향이 다른 주식을 혼합하여 투자하였을 때 위험을 완전히 없애거나 줄일 수 있음)
자산 A, B: 환율 변동에 따라 수익률에 영향을 줌
자산 C: 환율 변동에도 고정적으로 5% 수익률을 달성
즉 위 예제에서의 위험 요인은 환율 (자산 C는 무위험 자산으로 간주될 수 O)
100만원을 자산 C에 투자하는 것과 50만원씩 각각 자산 A와 B에 투자하는 것은 같은 결과 (분산투자의 원리)
두 자산에 분산하여 투자함으로써 위험을 줄일 수 있음
자산 C에만 투자: 1,050,000원 회수
환율 하락 시 A, B에 각각 50먼원 투자: A 45만원, B 60만원 회수
환율 상승 시 A, B에 각각 50만원 투자: A 60만원, B 45만원 회수
미래에 환률 상승/하락 혹은 위험 부담에 따라 투자할 자산이 달라짐. —> 자산의 특성을 충분히 파악한 후 자신의 수요와 목적에 맞는 투자 수단을 고르는 것이 자산 선택의 일반적인 원리



포트폴리오
- 서류 가방, 자료 수집철
- (재무) 여러 가지 자산으로 구성된 집합체
- N개 자산 포트폴리오: P=(w1, w2, ..., wn), n개의 가중치를 가지는 벡터를 포트폴리오로 나타낼 수 있음.
- wi은 i번째 자산에 배분된 비중
- ex) Wa가 50%, Wb가 50%일 때 각각 0.5의 가중치를 갖는 포트폴리오가 됨. 이것에서 가중치의 모든 합계는 1이 됨을 알 수 있음.
포트폴리오 이론
투자자가 추구하는 목적 달성을 위한 최적의 포트폴리오 선택에 관한 계량적, 분석적 이론 체계
- 주어진 위험 수준에서 기대수익률을 극대화하는 포트폴리오 선택
- 분산투자의 원리를 적용하여 최적의 위험관리를 수행
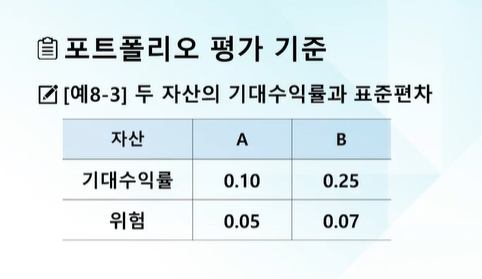
포트폴리오 평가 기준
- 수익성 : 수익률의 기대값(평균) 즉, 기대수익률
- 위험성 : 수익률의 분산 or 표준편차
- 기대수익률과 위험(표준편차)는 상충(trade-off)관계
Markowitz 평균-분산 기준(mean-variance criterion)
- 일정한 기대수익률에 대해 위험을 최소화하거나, 일정한 위험에 대해서 기대수익률을 최대화
ex) 위험이 동일한 자산 A, B가 있다면, 기대수익률이 더 높은 B가 더 선호됨
ex) 기대수익률이 동일한 자산 A, C가 있다면, 위험성이 적은 A가 선호됨
- 지배원리 : B라는 위험자산이 A라는 자산을 dominate한다
- 평균-분산 기준을 가지고 지배 원리에 의해서, 포트폴리오에 대해 투자자가 평가
분산투자를 이용한 포트폴리오
ex) 기대수익률의 목표치를 고정시키고, 이에 맞춰 위험 수준을 낮출 수 있는 포트폴리오를 구성
(투자자의 선호에 따라)

*p : 상관계수
p = 1일 때 A와 B를 분산투자한 포트폴리오 → A와 B를 잇는 직선 위의 한 점
p = 0.5일 때 A와 B를 분산투자한 포트폴리오 → 왼쪽으로 조금 치우친 곡선 위의 한 점
p = -1일 때 A와 B를 분산투자한 포트폴리오 → 위험이 0이 됨. 직선 위의 한 점
'가치를 창출하는 데이터 분석 > 금융 데이터 분석 (금융학회)' 카테고리의 다른 글
| [Financial Data] 금융경제학 Basic #22 시장 포트폴리오 (0) | 2023.10.24 |
|---|---|
| [Financial Data] 금융경제학 Basic #21 무위험자산을 위한 포트폴리오 (0) | 2023.10.24 |
| [Financial Data] 금융경제학 Basic #19 위험과 수익률 (0) | 2023.10.23 |
| [Financial Data] 금융경제학 Basic #18 기대 효용 이론 (0) | 2023.10.21 |
| [Financial Data] 금융경제학 Basic #17 위험태도와 화폐의 효용함수 (0) | 2023.10.21 |



