
안녕하세요!
이번에는 저번 주 포스팅에 이어서
팀 프로젝트의 두번째 진행에 대한 포스팅을 가져왔습니다!!
지난주의 포스팅을 아직 못보셨다구요??
그렇다면 아래 링크로 클릭 🔻🔻
[삼성 SDS Brightics]# 03-1. 팀프로젝트(1) 의료비(보험비) 예측
안녕하세요! 오늘은 브라이틱스 서포터즈 3기 5팀의 팀 프로젝트 첫번째 진행에 대한 포스팅을 가져왔습니...
blog.naver.com
1. 팀 분석 프로젝트 역할
이번 주의 저의 역할을 소개해드리자면,
'log변환과 정규성 검정, Split Data' 을 맡았습니다!
팀 분석 프로젝트이기에 각자의 역할을 수행하며
저의 역할을 구체적으로 공부할 수 있어 좋은 것 같습니다 :)
그렇다면 이제 시작해볼까요~?
목차는 다음과 같이 진행됩니다.

2. 로그 변환 (log 변환)
저는 전처리 이후 데이터에 대해 log 변환을 먼저 수행했습니다.
데이터 분석에서 로그 변환을 하는 경우가 종종 있는데요.
그 이유는 바로 정규성을 높이고, 분석에서 보다 정확한 값을 얻기 위해서 입니다! 😀😀
보통 왜도와 첨도로 인해 한쪽으로 편향되어있을 때, 데이터 간의 편차를 줄이기 위해 수행하게 됩니다.
그렇다면! 저희 의료비의 히스토그램을 먼저 봐볼까요?
1.1. charges(의료비)에 대한 히스토그램

charges(의료비)에 대한 히스토그램입니다.
시각화를 보니 정규 분포를 따르지 않고
한쪽으로 치우쳐진 양상을 볼 수 있죠?
(바로 skew하다고 합니다! )
정규성을 높이고 분석에서
보다 정확한 값을 얻기 위해서는
로그변환을 해줘야 하는 것을 볼 수 있습니다.
하지만 히스토그램으로만 보기에는
정규성을 만족하는지 알 수 없겠죠?
그렇기 때문에 로그 변환에 앞서 정규성 검정을 먼저 수행하고자 합니다 :)
여기서 '정규성 검정'이란?
측정하고자 하는 데이터셋의 분포가 정규분포를 따르는지를 검정하는 것입니다.
* 여기서 정규분포는 중심을 기준으로 좌우 대칭으로 나타나는 형태를 의미합니다.
1.2. charges(의료비)에 대한 AD Test
정규성 검정 중 Anderson-Darling (AD) test 입니다.
- 귀무가설(H0) : 표본 분포는 특정 분포를 따른다.
- 대립가설(H1): 표본 분포는 특정 분포를 따르지 않는다.
Anderson-Darling(AD) 통계량은 데이터가 특정 분포를 얼마나 잘 따르는지를 측정합니다.
일반적으로 AD 통계량이 작을수록 특정 분포를 잘 따른다고 볼 수 있습니다.
브라이틱스에는 Normality Test 안에
Kolmogorove-Smirnov test와
Jarque-Bera test, Anderson- Darling test가 있습니다.
(기회가 된다면, 브라이틱스에서 소개된 정규성 검정에 대해 따로 포스팅을 하도록 하겠습니다 💙)

결과를 보니 estimates가 85가 나왔죠?
높은지에 대해서는 아직 의문이지만,
이 후 추정량과 비교해보겠습니다 :)
1.3. charges(의료비)에 대한 Q-Q plot
이는 정규 분포를 따르는지를 시각화를 통해 확인하는 작업인데요.
아래 그림과 같이 Distribution Type을 Normal로 하게되면 정규분포를 따르는지 확인할 수 있습니다 :)

여러 기능에 한번더 감탄!!
브라이틱스는 기능이 옴총 많다..!!
Q-Q Plot도 이쁜 것은 무슨 이유..??

왼쪽은 Normal Distribution에 대한, 오른쪽은 log-normal Distribution으로 확인한 그래프입니다.
Normal Distribution의 경우,
연두선을 크게 벗어나는 것을 볼 수 있습니다.
log-normal Distribution의 경우,
연두선 내에서 희미하게 움직이는 것을 볼 수 있습니다.
이처럼 log-normal distribution
다시 말해 정규분포보다 로그분포에 더 가까운 것을 볼 수 있습니다!
그리하여 저는 charges 컬럼을 python script에서
numpy의 기능 중 하나인 np.log1p를 사용하여 로그 변환을 해주었습니다.

그렇다면 앞서 진행했던 시각화와 검정을 해봐야겠죠? 😀😁
2.1. log_charges(로그 변환 의료비)에 대한 히스토그램
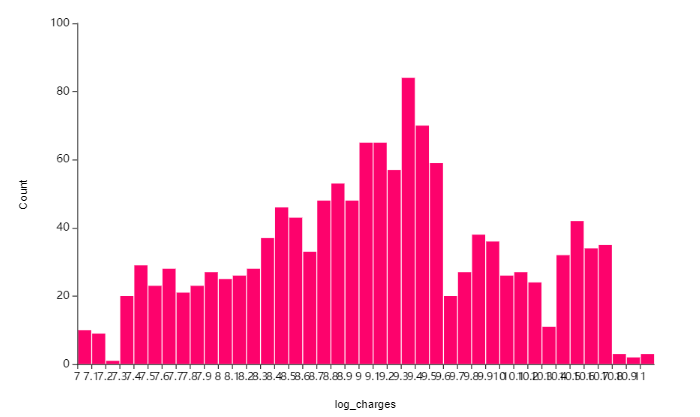
아까보다 데이터가 고르게 퍼진 것을 볼 수 있죠?
완벽한 정규분포에 따르지는 않아도
한쪽으로 치우쳐진 경향이 발생하지 않음을 볼 수 있습니다 😎
이제 정규성을 만족하는지 시각화를 통해 알아보겠습니다!
2.2. charges(의료비)에 대한 Q-Q plot

로그 변환 전의 Q-Q Plot과 비교했을 때 많이 달라짐을 확 느낍니다!
연두 선 안에 log_charges(빨간색)이 들어있는 것을 확인하니 마음이 편안..
2. 3. charges(의료비)에 대한 AD Test

결과를 확인하니 85에서 3.93으로 추정량이 작아진 것을 볼 수 있습니다.
(이전보다 특정 분포를 따른다고 볼 수 있습니다.)
이처럼 log 변환의 전과 후로 정규성의 유무가 결정되는 것을 확인해보았습니다!!
데이터 분석에 있어 데이터에 대한 검정은 빠질 수 없는데요.
정규성을 확인하기 위해서는 히스토그램과 Q-Q plot 그리고 정규성 검정이 있다는 것을 명심하세요! :)
이렇게 데이터 전처리가 끝이 났습니다!
그렇다면 무엇을 해야할까요? 바로바로.. 모델링이죠!!
하지만 데이터 전처리가 마무리가 되면, 모델링을 수행하기 전에 데이터를 분리하게 되는데요.
이를 split data 함수를 사용하여 분리하였습니다.
3. Split Data
Split data란 ?
무작위 row를 추출하여 데이터를
train set과 test set으로 나눌 때 사용하는 함수입니다!
저희는 train set과 test set을 7:3으로 나누어 진행하였습니다.
( 브라이틱스의 default 값..)

seed는 임의 추출 결과를 고정할 때 사용합니다.
아래 그림과 같이 1338개의 데이터를 7:3으로
936개의 train set과 402개의 test set으로 나눴습니다.

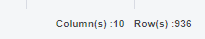
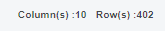
무작위로 진행하다보니, 결과값이 train을 돌릴 때마다 달라질 수 있는데요.
이는 교차검증을 사용하여 과적합과 과소적합을 막아
일반적인 모델을 구성하도록 하려고 합니다.
어떻게 하는지 궁금하시다구요~??
바로바로..
다음주를 기대해주세요!!
4. 느낀 점
이렇게 정규성 검정과 로그 변환
그리고 split data까지 진행을 하였는데요.
팀 프로젝트를 하면 항상 느끼는 것이지만
팀원들에게 배울 점이 많은 것 같습니다.
배려심과 친절은 물론이고.
제가 놓치는 부분을 잡는 역할까지 해주기에
팀 프로젝트를 하는 것 같습니다 :)
특히나 우리 팀원들과 소통하며
더욱 돈독해지고 친해져서 좋습니다~!! ㅎ_ㅎ
(나만 친한거 아니죠..?)
다음 주면 모델링과 최적화를 통해
모델을 구성한 뒤
팀 분석 프로젝트에 대한
포스팅이 마무리가 됩니다.
마지막까지 기대해주세요~!!
본 포스팅은 삼성SDS Brightics 서포터즈 3기 활동의 일환으로 작성하였습니다.
'가치를 창출하는 데이터 분석 > Brightics AI 데이터 분석' 카테고리의 다른 글
| [삼성 SDS Brightics]# 03-4. 팀프로젝트(4) 의료비 예측 마무으리!! (0) | 2022.09.06 |
|---|---|
| [삼성 SDS Brightics]# 03-3. 팀프로젝트(3) 의료비(보험비) 예측 (0) | 2022.08.30 |
| [삼성 SDS Brightics]# 03-1. 팀프로젝트(1) 의료비(보험비) 예측 (0) | 2022.08.16 |
| [삼성 SDS Brightics]# 02-3. 개인프로젝트(3) Kaggle 평균 기온 예측하기 - 시계열 분석 (ARIMA / Hot-Winters) (0) | 2022.07.13 |
| [삼성 SDS Brightics]# 02-2. 개인프로젝트(2) Kaggle 평균 기온 예측하기 - 시계열 분석 (MA / EWMA) (0) | 2022.07.05 |



