딥러닝을 이용한 자연어처리 입문 # 7. 머신 러닝 개요 4) ~ 6)
4) 자동 미분과 선형 회귀 실습
1. 자동 미분
tape_gradient() : 자동 미분 기능 수행
import tensorflow as tf
w = tf.Variable(2.)
def f(w):
y = w**2
z = 2*y + 5
return z
#gradients: w에 대해 미분한 값이 저장
with tf.GradientTape() as tape:
z = f(w)
gradients = tape.gradient(z, [w])
print(gradients)
# [<tf.Tensor: shape=(), dtype=float32, numpy=8.0>]
2. 자동 미분을 이용한 선형 회귀 구현
# 학습될 가중치 변수를 선언
w = tf.Variable(4.0)
b = tf.Variable(1.0)
#가설을 함수로 정의
def hypothesis(x):
return w*x + b
#임의로 입력값을 넣음
x_test = [3.5, 5, 5.5, 6]
print(hypothesis(x_test).numpy())
#결과 [15. 21. 23. 25.]
#손실 함수 정의(평균 제곱 오차)
def mse_loss(y_pred, y):
# 두 개의 차이값을 제곱을 해서 평균을 취한다.
return tf.reduce_mean(tf.square(y_pred - y))
#사용할 데이터
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 공부하는 시간
y = [11, 22, 33, 44, 53, 66, 77, 87, 95] # 각 공부하는 시간에 맵핑되는 성적
#옵티마이저 설정:경사 하강법, 학습률=0.01
optimizer = tf.optimizers.SGD(0.01)
for i in range(301):
with tf.GradientTape() as tape:
y_pred = hypothesis(x)
# 평균 제곱 오차를 계산
cost = mse_loss(y_pred, y)
# 손실 함수에 대한 파라미터의 미분값 계산
gradients = tape.gradient(cost, [w, b])
# 파라미터 업데이트
optimizer.apply_gradients(zip(gradients, [w, b]))
if i % 10 == 0:
print("epoch : {:3} | w의 값 : {:5.4f} | b의 값 : {:5.4} | cost : {:5.6f}".format(i, w.numpy(), b.numpy(), cost))
'''
epoch : 0 | w의 값 : 8.2133 | b의 값 : 1.664 | cost : 1402.555542
... 중략 ...
epoch : 280 | w의 값 : 10.6221 | b의 값 : 1.191 | cost : 1.091434
epoch : 290 | w의 값 : 10.6245 | b의 값 : 1.176 | cost : 1.088940
epoch : 300 | w의 값 : 10.6269 | b의 값 : 1.161 | cost : 1.086645
'''#학습된 w와 b의 값에 대해 테스트
x_test = [3.5, 5, 5.5, 6]
print(hypothesis(x_test).numpy())
#결과 [38.35479 54.295143 59.608593 64.92204 ]
3. 케라스로 구현하는 선형 회귀
케라스로 모델을 만드는 기본적 형식
- sequential로 model 생성
- add를 통해 입출력 벡터 추가
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 공부하는 시간
y = [11, 22, 33, 44, 53, 66, 77, 87, 95] # 각 공부하는 시간에 맵핑되는 성적
model = Sequential()
# 출력 y의 차원은 1. 입력 x의 차원(input_dim)은 1
# 선형 회귀이므로 activation은 'linear'
model.add(Dense(1, input_dim=1, activation='linear'))
# sgd는 경사 하강법을 의미. 학습률(learning rate, lr)은 0.01.
sgd = optimizers.SGD(lr=0.01)
# 손실 함수(Loss function)은 평균제곱오차 mse를 사용합니다.
model.compile(optimizer=sgd, loss='mse', metrics=['mse'])
# 주어진 x와 y데이터에 대해서 오차를 최소화하는 작업을 300번 시도합니다.
model.fit(x, y, epochs=300)
#오차를 최소화하는 직선 그래프화
plt.plot(x, model.predict(x), 'b', x, y, 'k.')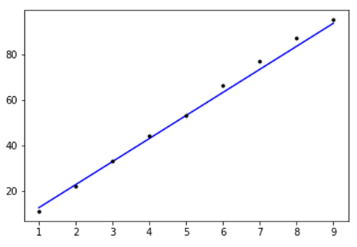
5) 로지스틱 회귀(Logistic Regression)
1. 이진 분류(Binary Classification)
- y가 0과 1 두가지 값만 가지므로 직선이 부적합함
- 0과 1 사이의 값을 가지면서 s자 형태로 그려지는 시그모이드 함수 이용
2. 시그모이드 함수
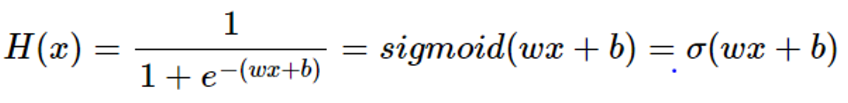
- 적합한 가중치(w)와 편향(B)를 구하는 것
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y, 'g')
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()
3. 비용 함수
- 로지스틱 회귀에서 평균 제곱 오차를 비용함수로 사용하면 문제 발생 → 특정 구역에서의 최소값인 로컬 미니멈에 빠질 가능성이 있음
- 로지스틱 회귀에서는 크로스 엔트로피 함수를 비용 함수로 사용
6) 텐서플로우를 사용한 로지스틱 회귀 실습
- 케라스로 구현하는 로지스틱 회귀
- 독립 변수 x
- 10 이상인 경우는 1, 미만인 경우는 0을 부여한 레이블 데이터 y
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
x = np.array([-50, -40, -30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50])
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]) # 숫자 10부터 1
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))
sgd = optimizers.SGD(lr=0.01) #경사 하강법 사용
model.compile(optimizer=sgd, loss='binary_crossentropy', metrics=['binary_accuracy'])
#손실 함수로 binary_crossentropy 사용, 에포크=200
model.fit(x, y, epochs=200)
#실제값과 오차가 최소화된 모델 그래프로 시각화
plt.plot(x, model.predict(x), 'b', x,y, 'k.')
print(model.predict([1, 2, 3, 4, 4.5]))
print(model.predict([11, 21, 31, 41, 500]))
[[0.21071826]
[0.26909265]
[0.33673897]
[0.41180944]
[0.45120454]]
[[0.86910886]
[0.99398106]
[0.99975663]
[0.9999902 ]
[1. ]]반응형
'공부하는 습관을 들이자 > Deep Learning (NLP,LLM)' 카테고리의 다른 글
| [딥러닝 자연어처리] 8. 1) 퍼셉트론 ~ 2) 2. 인공 신경망 훑어보기 (0) | 2023.12.14 |
|---|---|
| [딥러닝 자연어처리] 7. 머신 러닝 개요 7) ~ 9) (0) | 2023.12.13 |
| [딥러닝 자연어처리] 7. 머신 러닝 개요 1) ~ 3) (0) | 2023.12.11 |
| [딥러닝 자연어처리] 6-1. 토픽 모델링 (0) | 2023.12.08 |
| [딥러닝 자연어처리] 5. 벡터의 유사도 (0) | 2023.12.06 |



