4.6 로지스틱 회귀
로지스틱 회귀(logistic regression)는 샘플이 특정 클래스에 속할 확률을 추정하는 데 널리 사용된다.
추정 확률이 50% 이상이면 모델은 그 샘플이 해당 클래스에 속한다고 예측, 아니면 클래스에 속하지 않는다고 예측한다. -> 이진 분류기이다.
4.6.1 확률 추정
로지스틱 회귀 모델은 입력 특성의 가중치 합에 편향을 더해 계산한다. 이때 선형 회귀처럼 바로 결과를 출력하지 않고, 결과값의 로지스틱(logistic)을 출력한다.

로지스틱은 0 과 1 사이의 값을 출력하는 시그모이드 함수(sigmoid function)이다.

이 함수를 거쳐나온 확률값으로 최종적으로 주어진 데이터가 어느 클래스에 속할지에 대해 결정하게 된다.
보통 확률값이 0.5 이상이면 1 (양성 클래스) , 이하면 0 (음성 클래스)라고 예측한다.
4.6.2 훈련과 비용 함수
훈련의 목적은 양성인 데이터 (y = 1)에 대해서는 높은 확률을 추출하고 음성인 데이터(y=0)에 대해서는 낮은 확률을 추출하는 것이다. 비용 함수는 이러한 아이디어를 잘 반영하고 있다.

예를 들어 데이터는 음성에 가까운데 양성 클래스로 예측하면 - log(t)는 매우 커지므로 잘못된 예측이라는 것을 알 수 있다. 혹은 데이터는 양성에 가까운데 음성 클래스로 예측하면 마찬가지로 -log(1-t)는 매우 커진다는 것을 알 수 있다.
반대로 t가 1에 가까워지면, -log(t)는 0에 가까워지고, t가 0에 가까워지면, -log(1-t)는 역시 0에 가까워진다.
전체 훈련 세트에 대한 비용 함수는 모든 훈련 샘플의 비용을 평균한 것이고 이를 로그 손실(log loss)라고 부르며 다음과 같은 식으로 표현된다.

--> 이 비용 함수의 최솟값을 알고 싶으나 계산하는 알려진 해는 없다. 하지만 이 비용 함수는 볼록 함수이므로 경사 하강법이 전역 최솟값을 찾는 것을 보장한다.

각 샘플에 대한 예측 오차를 계산하고 j번째 특성값을 곱해 모든 훈련 샘플에 대해 평균을 낸다. 모든 편도함수를 포함한 그레이디언트 벡터를 만들면 배치 경사 하강법 알고리즘을 사용할 수 있다.
4.6.3 결정 경계

세 개의 품종을 로지스틱 회귀로 분류하는 예시이다. 우리가 사용할 데이터에는 꽃잎, 꽃받침의 너비와 길이를 담고 있다. 여기서는 꽃잎의 너비를 기반으로 Iris-Versicolor종을 감지하는 분류기를 만들어볼 것이다.
데이터 로드
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
>>
['data','target','frame','target_names','DESCR', 'feature_names','filename']
X = iris["data"][:, 3:] # 꽃잎 너비
y = (iris["target"] == 2).astype(np.int) # Iris virginica이면 1 아니면 0로지스틱 회귀 모델 훈련
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)꽃잎의 너비가 0~3cm인 꽃에 대해 모델의 추정 확률을 계산
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
save_fig("logistic_regression_plot")
plt.show()
- Iris-Verginica의 꽃잎 너비는 1.4cm~2.5cm 사이. 반면 다른 꽃들의 꽃잎 너비는 0.1 ~ 1.8cm 사이로 약간 중첩된다.
- 꽃잎의 너비가 2cm가 넘어가면 Iris-Verginica라고 강하게 확신한다.
- 양쪽의 확률이 똑같이 50%가 되는 1.6cm 근방에서 결정 경계(decision boundary)가 생성된다. 바로 이 결정 경계를 기준으로 꽃잎의 너비가 크면 Iris-Verginica라고 예측할 것이다.
1.7은 양성, 1.5는 음성
log_reg.predict([[1.7], [1.5]])array([1, 0])
선형 결정 경계
from sklearn.linear_model import LogisticRegression
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.int)
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1),)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")
zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]
plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
save_fig("logistic_regression_contour_plot")
plt.show()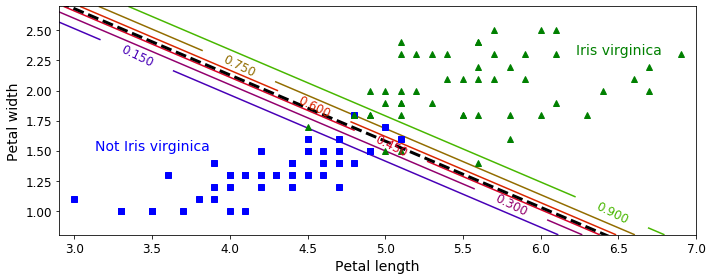
- 검은색 점선 : 결정 경계
- 초록색 선 위 : 90% 이상의 확률로 Iris-Verginica (양성 클래스) 로 분류된 데이터
- 파란색 선 아래 : 15% 미만으로 not Iris-Verginica (음성 클래스)로 분류된 데이터
4.6.4 소프트맥스 회귀
여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화될 수 있다.
이를 소프트맥스 회귀(softmax regression) 또는 다항 로지스틱 회귀(multinomial logistic regression)이라고 한다.
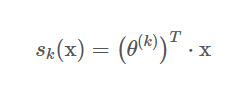
데이터가 주어지면 소프트맥스 회귀 모델은 해당 데이터가 각 클래스에 대한 점수를 계산하고, 소프트맥스 함수를 이용하여 이 점수를 확률값으로 바꾸게 된다. 그리고 가장 높은 확률값을 가진 클래스로 데이터 x를 분류하게 된다.
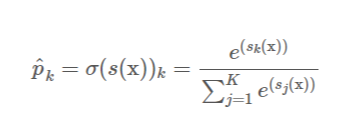
- K는 클래스 수이다.
- s(x)는 샘플 x에 대한 각 클래스의 점수를 담은 벡터이다.
- s(x)의 표준편차는 샘플 x에 대한 각 클래스의 점수가 주어졌을 때 이 샘플이 클래스 k에 속할 추정 확률이다.
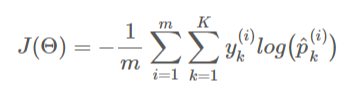
훈련 목적은 타깃 클래스에 대해서는 높은 확률을, 나머지는 낮은 확률을 추정하도록 하는것이다.
여기에 크로스 엔트로피 비용함수(Cross-Entropy Cost 함수)를 사용한다. 그리고 이를 최적화하기 위한 Gradient Vector는 다음과 같다.
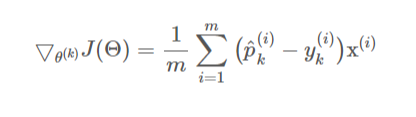
소프트맥스 회귀 적용
X = iris["data"][:, (2, 3)] # 꽃잎 길이, 꽃잎 너비
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)꽃잎의 길이가 5cm, 너비가 2cm인 꽃의 품종이 무엇인지 모델에 질의하면 94.2% 확률로 Iris-Verginica라고 출력한다.
softmax_reg.predict([[5, 2]])
>> array([2])softmax_reg.predict_proba([[5, 2]])
>> array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])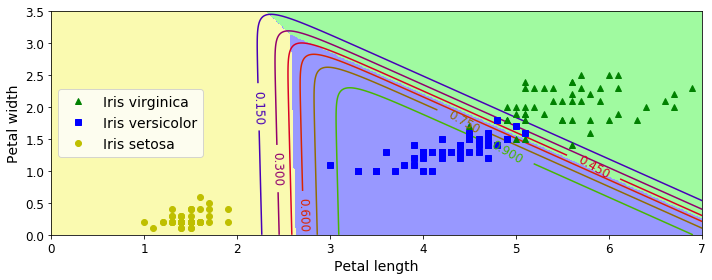
클래스 사이의 결정 경계는 모두 선형이다. 또한 Iris-Versicolor 클래스에 대한 확률을 곡선으로 나타낸다.
모든 결정 경계가 만나는 지점에서는 클래스가 모두 동일하게 33%의 추정 확률을 가진다.
자세한 코드는 저의 깃허브를 참고하시면 됩니다.
https://github.com/rootofdata/handson-ML
GitHub - rootofdata/handson-ML: handson ML
handson ML. Contribute to rootofdata/handson-ML development by creating an account on GitHub.
github.com
참고 문헌 :
https://book.naver.com/bookdb/book_detail.nhn?bid=16328592
핸즈온 머신러닝
머신러닝 전문가로 이끄는 최고의 실전 지침서 텐서플로 2.0을 반영한 풀컬러 개정판 『핸즈온 머신러닝』은 지능형 시스템을 구축하려면 반드시 알아야 할 머신러닝, 딥러닝 분야 핵심 개념과
book.naver.com
'공부하는 습관을 들이자 > Machine Learning For Study' 카테고리의 다른 글
| Hands-on ML : 5.2 비선형 SVM 분류 (0) | 2022.06.02 |
|---|---|
| Hands-on ML : 5.1 선형 SVM 분류 (0) | 2022.05.26 |
| Hands-on ML : 4. 5 릿지(Ridge),라쏘(Lasso),엘라스틱 넷(Elastic-net) 모델 훈련 (0) | 2022.05.20 |
| Hands-on ML : 4. 3 다항회귀 및 4.4 학습곡선 (0) | 2022.05.19 |
| Hands-on ML : 4. 2 확률적 경사하강법, 미니배치 경사 하강법 (0) | 2022.05.18 |



