Deep-Compact-
Clustering Based Anomaly Detection Applied to Electromechanical Industrial Systems
본 논문은 MDPI 논문이며, sensors 저널에 등록된 논문이다. Impact Factor는 4.35이며,
Unsupervised anomaly detection으로 클러스터링을 이용한 이상값 감지 방법론이다. 또한 LSTM을 기반으로 한 Autoencoder을 쓰기에 이상치 탐지에 적합하다고 생각했다.

아래 그림은 DAECC-DC-SVM 방법의 틀로서, 제안된 이상 탐지 모니터링 방법론의 단계별 흐름도이다.

3. Methodology
3.1. Data Acquisition
제안된 방법론의 첫 번째 단계는 회전 시스템의 상태와 관련된 정보 수집과 관련이 있다. 제안된 방법론은 1초 세그먼트에 대한 물리적 크기의 특성화를 기반으로 한다. 이와 관련하여 이 기간 동안의 정적 동작을 고려하면 이 획득 시간은 대부분의 실제 적용(즉, 500rpm보다 큰 회전 속도)에서 충분한 통계적 일관성을 보장한다. 그러나 이러한 저속 응용 프로그램의 성능 손실을 방지하기 위해 획득 시간을 늘릴 수 있다. 전기 기계 시스템의 조건에 대해, 본 방법론은 제시될 수 있는 토크 및 속도 변형을 포함하여 정상적인 작동 조건에 해당하는 데이터로 시작하도록 설계되었다. 어떤 경우에도 획득 세부 정보가 동일한 한 다른 작동 상태(즉, 결함 및 성능 저하 수준)에 해당하는 획득을 추가할 수 있다. 따라서 이 단계의 결과는 원시 진동 신호다.
3.2. Signal Pre-Processing
이 필터링 프로세스의 주요 목적은 추가 처리에 적합한 형태의 진동 신호를 얻는 것이다. 이러한 의미에서 신호의 각 분할된 부분은 1500Hz와 동일한 차단 주파수로 저역 통과 필터링 단계를 개별적으로 처리했다. 필터링 프로세스 후에 신호의 스펙트럼은 FFT(고속 푸리에 변환)를 사용하여 얻는다. 따라서 각 신호 세그먼트에 대해 해당 주파수 진폭을 얻는다. 마지막으로 주파수 계수가 조정되어 모델의 최종 입력으로 사용된다.
주파수 진폭이 너무 작아 네트워크 가중치를 변경하지 못하기 때문에 [46]의 권장 사항에 따라 샘플에 계수를 곱한다. 데이터 세트와 관련하여 세 부분으로 나뉜다. 첫 번째 부분은 훈련 목적으로 사용 가능한 샘플의 70%로 구성되고 두 번째 부분은 검증 목적으로 사용 가능한 샘플의 20%로 구성되며 마지막으로 세 번째 부분은 10%로 구성된다. 테스트 목적을 위한 샘플의 %. 또한 결과가 통계적으로 유의하다는 것을 확인하기 위해 5중 교차 검증 접근 방식이 데이터에 적용된다. 이 단계에서 결과는 필터링되고 주파수 성분으로 변환된 진동 신호의 세그먼트이다.
3.3. Train Deep-Autoencoder
본 논문에서는 [47]에서 제안한 DAE 아키텍처를 레이어별로 학습하였다. L2 정규화 항에 대한 계수, 희소성 정규화 항에 대한 계수, 희소성 비율에 대한 매개변수 및 각 은닉층의 뉴런 수와 같은 DAE 하이퍼파라미터는 최적의 검색을 통해 설정된다. 유전 알고리즘(GA)을 사용한 구성. 최적화 절차는 다음과 같이 수행된다.
- Population initialization: GA의 염색체는 처음에 5개의 요소를 포함하는 논리 벡터로 정의된다. 각 요소는 세 개의 하이퍼파라미터와 두 개의 은닉층에 있는 뉴런 수이다. 그 후, 각 특정 매개변수에 특정 값을 할당하여 모집단의 무작위 초기화를 수행한다. 사실, 각 매개변수에 할당된 값은 미리 정의된 값 범위 내에 있다. 모집단 초기화가 완료되면 절차는 2단계에서 계속된다.
- Population assessment: 이 단계에서는 입력 및 출력 특성 간의 재구성 오류 최소화를 기반으로 하는 적합성 함수를 평가한다. (함수는 논문 2.1절 (1) 참고) 따라서 GA의 목표는 재구성 오류를 최소화하는 것이다. 따라서 GA로 해결해야 하는 최적화 문제는 고성능 기능 매핑을 이끄는 특정 매개변수 값의 검색을 포함한다. 그런 다음 전체 모집단이 광범위한 값으로 평가되면 최상의 매개변수 값의 조건을 분석하고 절차는 4단계로 계속된다.
- Mutation operation: GA의 돌연변이는 룰렛 휠 선택을 통해 인구의 새로운 값을 생성하고, 새로 생성된 인구는 이전 평가된 인구에 의해 달성된 최상의 적합도 값의 선택을 고려한다. 또한 새로운 모집단을 생성하는 동안 가우스 분포를 기반으로 하는 돌연변이 연산이 적용된다. 그 후 절차는 2단계에서 계속된다.
- Stop criteria: GA에 대한 정지 기준은 다음 두 가지다. 첫 번째 중지 기준(i)의 경우 GA가 진화할 때까지 최적의 매개변수 값이 발견될 때까지 절차를 반복적으로 반복한 다음 절차 3에서 절차를 계속한다.
이후 입력 계층은 처리를 통해 얻은 FFT 데이터의 길이에 해당하며, 이는 네트워크 학습에 사용된다. 출력 레이어는 2차원 특징 공간을 생성하기 위해 2로 설정된다. 확률적 경사하강법의 확장인 Adam 최적화 알고리즘은 손실 함수를 최적화하는 데 사용된다[48]. 가중치는 Xavier uniform initializer라고도 하는 Glorot uniform initializer를 사용하여 초기화되며, 이는 입력 및 출력 뉴런의 수에 따라 초기화 규모를 자동으로 결정한다[49]. 활성화 함수는 시그모이드 함수로 설정된다. DAE 훈련은 비지도학습이므로 입력 데이터의 레이블 정보가 필요하지 않다.
따라서 최종 DAE 구조는 훈련 과정에서 사용된 FFT 신호를 효과적으로 재구성할 수 있으며 동시에 병목 코딩 계층은 2차원 공간에서 투영될 수 있는 특징 공간을 생성할 수 있다. 인코더 출력은 모든 사용자가 해석할 수 있는 기능 공간을 생성하기 위해 2차원으로 선택된다. DAE 프레임워크의 두 기능 모두 이상 감지에 사용할 수 있다. 한편으로는 훈련 중에 사용된 신호를 재구성하고 재구성 오류를 측정하는 기능이 있다. 반면에 경계를 구축하고 변칙 구성원을 설정할 수 있는 기능 공간 매핑 생성이 가능하다. 비정상 멤버십은 OCC 기반 스키마의 구현에 따라 다르다. 2차원 투영으로 작업할 때 이상 구성원은 알려진 데이터가 포함된 경계로 생성될 수 있지만 이상은 해당 구성원 또는 경계 외부에 있다. 이 단계의 결과는 특징 공간과 입력 신호의 효과적인 재구성을 모두 생성할 수 있는 훈련된 AE 모델이다.
3.4. Train Deep-Compact Clustering
DAE 모델은 병목 코딩 계층의 출력에서 특징 공간 매핑을 생성하는 기능이 있지만 DAE는 OCC 문제에 직접 적용할 때 비효율적일 수 있다. 병목의 특징 공간 매핑이 희소할 수 있기 때문이다. 바람직한 결과를 위한 OCC 문제에서 필수적인 문제인 병목에서 데이터의 간결한 매핑이다[36]. 이와 관련하여 특징 공간에서 클러스터의 압축성을 향상시키기 위한 프레임워크로 적용된다. 본 연구에서 소개된 deep-compact-clustering은 [40]에서 제시한 개념을 따른다. 클러스터는 DAE 인코더의 동일한 아키텍처로 심층 신경망을 초기화하기 위해 DAE 교육 중에 학습된 가중치를 사용하여 구성되고 디코더 부분은 버린다. DCC의 목표는 반복적이고 비지도학습의 프로세스를 통해 기능 공간 매핑과 클러스터 중심을 동시에 최적화하는 것이다. 중심은 퍼지 C-평균 알고리즘을 사용하여 초기화되며 k는 사용자 정의 매개변수이다. 이 작업에서 k 중심은 연구 중인 전기 기계 시스템의 알려진 작동 조건(즉, 획득 단계에서 고려되는 토크 및 속도 설정) 각각에 해당한다는 것이 설정되었다. DCC 모델은 학습률이 0.001이고 배치 크기가 200으로 설정된 표준 역전파 절차에서 모멘텀이 있는 Adam 최적화 프로그램을 사용하여 훈련 단계의 모든 데이터 세트에 사용된다. 스튜던트 t-분포의 자유도 α는 하나로 설정된다. 이와 관련하여 이 단계의 결과는 컴팩트 클러스터가 있는 기능 공간이다.
3.5. Train Oc-svm
다음 단계는 OCC 방식을 수행하는 것이다. DCC 최적화로 인해 특징 공간에 압축된 클러스터는 OCC 방식을 훈련하는 데 사용된다. 현재 방법론에서 OC-SVM은 이상 분류기로 사용된다. OC-SVM 매개변수를 설정하기 위해 조합 검색 전략이 사용된다[50]. 커널 및 정규화 매개변수는 실험을 통해 얻는다. 5중 교차 검증이 최상의 결과를 결정하는 데 사용된다. RBF 커널은 모든 사례 연구에 사용된다.
매개변수가 정의되고 최적화가 수렴되면 OC-SVM은 알려진 시나리오(정상 및 결함 세트)의 정보로 훈련되지만 고유 클래스로 레이블이 지정된다. 이는 모델이 이상 구성원이라고 하는 알려진 모든 시나리오를 포함하는 경계를 찾는다. 양수 값은 주어진 데이터 포인트가 평면 내에 있음을 나타내고(정상치로 간주됨), 반대로 음수 값은 결정 경계 밖에 있음을 나타낸다(이상치로 간주됨).
3.6. Reconstruction Model
재구성 모델의 기본 아이디어는 시스템의 입력과 동일한 출력을 재생성 하는 것이다. 이러한 의미에서 이미 2.1에서 논의한 바와 같이 AE는 데이터를 피쳐 공간에 최적으로 매핑하도록 학습하고 작은 재구성 오류(예: ΩMse)로 재구성하도록 훈련된 모델이다. 이 데이터는 시스템의 공칭 상태에 관한 것일 수 있다. 그러나 특성 공간에 대한 매핑이 최적화되지 않았으므로 결과적으로 재구성 오류가 상당히 높아진다. DAE는 알려지지 않은 데이터에도 적합할 수 있으므로 데이터의 품질, 다양한 작동 조건 및 훈련 데이터에 대한 적합 수준은 고려해야 한다. 이 경우 이상 데이터에 대한 재구성 오류는 명목 데이터에 대한 오류만큼 낮을 수 있으며 이는 바람직하지 않은 결과이다. 이 단계에서 재구성 오차 측정을 기반으로 한 이상 점수가 최종 결과이다.

3.7. Decision Rule
먼저, OC-SVM을 통해 feature space mapping에 대한 anomaly Membership과 재구성 과정을 통해 얻은 anomaly score를 분류 결과 자체로 사용할 수 있다. 그러나 두 방법 모두 이상 탐지에 대해 잘못될 수 있다. 한편, 비정상적인 데이터의 경우 클러스터 압축 프로세스에도 불구하고 피쳐 공간에 대한 매핑이 최적화되지 않았지만 알려진 샘플에서 데이터 중복이 발생할 수 있다. 반면에, 재구성 오차 측정은 이상으로 간주된 데이터가 명목 데이터의 재구성 값에 적합할 수 있고 오차 값이 높은 샘플만 외부에서 감지되기 때문에 비정상 샘플을 감지하지 못할 수 있다. 임계값 및 따라서 변칙으로 간주된다. 이와 관련하여 본 방법론에서는 DAE의 심층 특징 표현 기능을 사용하여 이상 탐지를 수행한 다음 OC-SVM과 함께 매핑 공간 압축 프로세스를 통해 클러스터의 품질을 향상시킨다. 그런 다음 탐지를 강화하기 위해 DAE의 재구성 프로세스에서 얻은 이상 점수를 사용한다. 따라서 주어진 샘플 X에 대해 OC-SVM의 이상 멤버십이 양수이면 정상으로 분류되며, 이는 샘플이 경계 내에 있음을 의미합니다. 대신 샘플 X는 다음과 같은 경우 비정상으로 분류됩니다.

여기서 AM(oc-svm)은 oc-svm의 anomaly membership이다. 따라서 알려진 샘플의 탐지 결과는 DCC+OC-SVM으로 이상 징후의 식별은 DCC+OC-SVM과 DAE를 통한 측정의 조합으로 이루어진다.
3.8. Validation
DAECC-OC-SVM의 이상 탐지 성능을 평가하기 위해 검증 및 테스트 데이터베이스를 사용하여 평가를 수행한다. TP(TruePositive)의 결과는 OC-SVM을 통해 anomaly score을 도출한다.
4. Validation and Analysis
4.1. Data
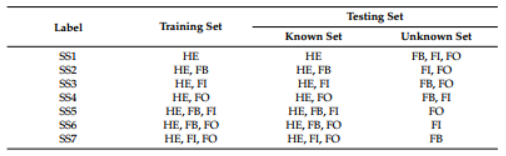
데이터 세트는 Case Western Reserve University의 베어링 데이터 센터에서 획득했다[54]. 그것은 건강한 데이터와 잘못된 데이터로 구성된 유도 전동기의 드라이브 끝에 장착된 가속도계를 사용하여 수집되었다. 결함 데이터 세트는 볼(FB), 내부 레이스(FI) 및 외부 레이스(FO)의 단일 포인트 결함에 의해 생성되었다. 각각의 결함에 대해 다양한 결함 심각도에 해당하는 세 가지 결함 크기(각각 0.007인치, 0.014인치 및 0.021인치)가 있다. 또한 다양한 모터 부하(0, 1, 2 및 3 hp)에 해당하는 서로 다른 작동 조건에서 데이터를 수집했다. 모든 데이터 세트는 12kHz의 샘플링 주파수로 수집되었다. 정상 조건 및 결함 조건과 같이 고려되는 각 조건에 대해 각각에 대해 200개의 샘플이 있다.
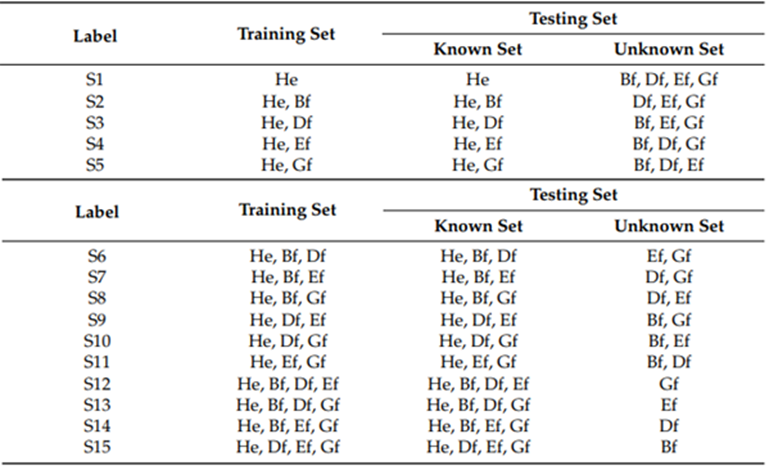
테스트를 위한 7가지 시나리오는 이상 시나리오를 감지하는 방법론의 능력과 초기에 사용 가능한 정보에 대한 새 클래스의 통합에 대한 모델의 응답을 평가하는 것으로 간주된다. 각 시나리오에 대한 클래스 분포는 표 2에 나와 있다. 4개의 클래스는 학습 세트, 알려진 세트 및 알 수 없는 세트의 세 가지 세트로 그룹화된다. 각각의 시나리오는 4가지 작동 조건으로 건강 상태(HE)만 아는 초기 지식에서 3가지 등급의 데이터를 알고 있는 시나리오까지 제안된 접근 방식의 진행 단계에 해당한다. 이러한 시나리오는 초기에 건강한 상태가 초기에 사용 가능하고 점진적으로 새로운 결함 상태가 감지 및 통합되는 실제 산업 프레임워크에서 제안된 방법론의 기능을 테스트하는 것을 목표로 한다. 이것은 각 진행 단계의 훈련 단계에 하나의 결함 상태가 추가되는 방식으로 수행된다.
4.2. Experimental Results
제안된 DAECC-OC-SVM 방법의 효과와 성능을 검증하기 위해 얻은 결과를 세 가지 대표적인 비지도 변칙 방법과 비교하였다. 먼저 참조 방법과 추가로 DAECC-OC-SVM의 두 가지 변형 단순:
- 참조 방법: deep-autoencoder를 사용한 재구성 모델[33,55];
- 변형 단순 방법 1: deep-autoencoder + OC-SVM;
- 변형 단순 방법 2: deep compact clustering + OC-SVM.
(1)은 섹션 3.6에 설명된 재구성 기반 방법이다. 여기서 임계값만 이상을 식별하는 메트릭으로 사용된다. 이 방법은 다른 응용 프로그램에서 성공적으로 구현되었다. (2)는 개선된 특징 공간 압축 과정 없이 deep-autoencoder 모델과 one-class support-vector 머신 기반의 이상 탐지 방법을 통합하는 방법이다. (3)은 DAECC-OC-SVM 방법의 단순화된 버전이다.(재구성 모델은 고려되지 않음).

예측치에서는 TNR(거짓을 거짓으로 보는 경우)이 높아야한다. 대부분의 TPR이 큰 반면 TNR은 대부분의 경우 0.5미만으로 알려져 있지 않은 클래스의 샘플 대부분을 감지할 수 없다. 또한 DCC를 통한 특징 공간의 압축으로 이상 탐지가 상당히 향상된다.
이와 관련하여 제안된 방법론은 특징 공간에서 클러스터의 압축성을 개선하여 OC-SVM 탐지 성능을 향상시키기 위해 DCC의 기능을 채택한다. 또한 DAE 재구성 기능을 결합하여 변칙 사례의 정확도를 향상시킬 수 있다. 따라서 제안하는 DAECC-OC-SVM 모델이 이상치 탐색에 있어 다른 모델보다 뛰어남을 볼 수 있다.
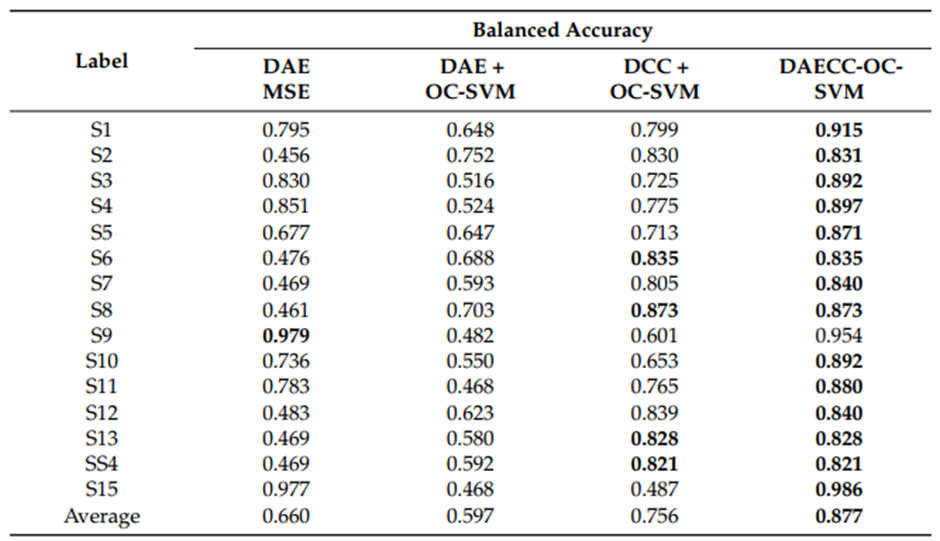
위 표는 상응하는 균형 정확도를 보여준다. DAECC-OC-SVM 기반 방법은 각 시나리오에서 다른 방법보다 우수하다. 4가지 시나리오(S6, S8, S13, S14)에서 단순화된 버전, 즉 DCC + OC-SVM에서만 정확도가 일치한다. 이는 재구성 모델(DAE MSE)이 이 네 가지 시나리오에서 비정상 샘플을 감지할 때 개선을 제공하지 않는다는 것을 의미한다.
4.2.2에서도 마찬가지로 DAECC-OC-SVM이 가장 높은 수치를 나타내므로 이하 생략한다.



