공부하는 습관을 들이자/Deep Learning (NLP,LLM)

[딥러닝 자연어처리] 7. 머신 러닝 개요 7) ~ 9)

꿀먹은데이터 2023. 12. 13. 15:32

딥러닝을 이용한 자연어처리 입문 # 7. 머신 러닝 개요 7) ~ 9)

7) 다중 입력에 대한 실습

크로스 엔트로피 함수를 이용해서 이를 이용해 가중치를 찾고, 가중치는 크로스 엔트로피 함수의 평균을 이용한 방식으로 사용. 크로스 엔트로피 함수는 소프트맥스 회귀의 비용 함수

import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
# 중간 고사, 기말 고사, 가산점 점수
X = np.array([[70,85,11], [71,89,18], [50,80,20], [99,20,10], [50,10,10]]) 
y = np.array([73, 82 ,72, 57, 34])

model = Sequential()
model.add(Dense(1, input_dim=3, activation='linear')) #input의 파라미터를 세 개로 받아

sgd = optimizers.SGD(lr=0.0001) #하강법에서 변수를 0.0001로 받아주고
model.compile(optimizer=sgd, loss='mse', metrics=['mse']) #mse를 기점으로
model.fit(X, y, epochs=2000)  #에포크 2000회 돌리기

8) 벡터와 행렬 연산

1. 벡터와 행렬과 텐서

  • 벡터 - 크기와 방향을 가진 양(배열 or list)
  • 행렬 - 2차원(행과 열로 구성)
  • 텐서 - 3차원

2. 텐서

 

0차원 텐서

  • 스칼라 - 하나의 실수값으로 이뤄진 데이터 ⇒ 0차원 텐서
d = np.array(5)
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)

# 텐서의 차원 : 0
# 텐서의 크기(shape) : ()

 

1차원 텐서(벡터)

  • 숫자를 배열한 것으로 4차원 벡터지만, 1차원 텐서로 불림
d = np.array([1, 2, 3, 4])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
텐서의 차원 : 1
텐서의 크기(shape) : (4,)

 

2차원 텐서(행렬)

  • 행과 열이 존재하는 벡터의 배열
d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
텐서의 차원 : 2
텐서의 크기(shape) : (3,4)

 

3차원 텐서

  • 행렬 또는 2차원 텐서를 한번 더 배열할 경우
d = np.array([
            [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [10, 11, 12, 13, 14]],
            [[15, 16, 17, 18, 19], [19, 20, 21, 22, 23], [23, 24, 25, 26, 27]]
            ])
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)
텐서의 차원 : 3
텐서의 크기(shape) : (2,3,5)

3D 텐서가 자연어 처리에서 많이 보이고, 시퀀스 데이터에서 자주 사용 (단어의 시퀀스)

3개의 훈련 데이터에서 인공 신경망의 모델로 이용하기 위해선 각 단어를 벡터화해야 함

  • 아래와 같이 훈련 데이터를 다수 묶어 입력에 이용하는 걸 배치라고 함

[[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0]],

[[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]],

[[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1]]]

 

그 이상의 텐서

  • 3D 텐서 → 배열화 → 4차원 텐서 → 배열화 → 5차원 텐서

케라스에서의 텐서

  • 각 numpy는 ndim과 shape를 출력
    • ex) 3차원 크기 → (2,3,5) → shape를 인자로 줄 때, input_shape를 사용.
  • input_shape를 보내줄 때 배치 크기는 제외하고, 차원을 지정해주는 것.
    • ex) input_shape(6, 5) 배치 크기 32 → 텐서 크기 (?, 6, 5)
  • 입력의 속성 수 = input_dim, 시퀀스 데이터 길이 = input_length
  • input_shape의 두 인자는 (input_length, input_dim).

3. 벡터와 행렬의 연산

벡터 계산
행렬 계산

벡터 내적

A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print('두 벡터의 내적 :',np.dot(A, B))

32 #np.dot를 이용

행렬 곱

A = np.array([[1, 3],[2, 4]])
B = np.array([[5, 7],[6, 8]])
print('두 행렬의 행렬곱 :')
print(np.matmul(A, B))
두 행렬의 행렬곱 :
[[23 31]
 [34 46]]
#np.matmul를 이용

4. 다중 선형 회귀 행렬 연산으로 이해하기

입력 행렬 X에 다양한 값이 포함되어 있다면 다음과 같이 X를 표현하고, 가중치 벡터 W의 곱으로 표현할 수 있음

여기다가 절편값까지 더해주면 H(X) = XW + B로 표현

5. sample과 feature

  • sample = 각각의 데이터 단위
  • feature = 각각의 독립 변수

6. 가중치와 편향 행렬의 크기 결정

  • 두 행렬의 곱 J × K이 성립되기 위해서는 행렬 J의 열의 갯수와 행렬 K의 행의 갯수는 같아야 한다.
  • 두 행렬의 곱 J × K의 결과로 나온 행렬 JK의 크기는 J의 행의 갯수와 K의 열의 갯수를 가진다.

다음과 같은 성질을 가지기 때문에 역으로 독립 행렬 혹은 가중치 행렬의 행과 열의 크기에 대해 정보가 부족할 때 이를 역으로 추산할 수 있다.

9) 소프트맥스 회귀

  • 3개 이상 선택지 중 1개를 고르는 다중 클래스 분류 문제.

1. 다중 클래스 분류

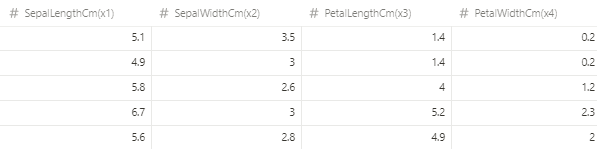
  • 받침 길이, 꽃받침 넓이, 꽃잎 길이, 꽃잎 넓이를 통해 3가지 품종 중 어떤 품종인 지 예측하는 문제.
  • 앞서 배운 시그모이드 함수를 이용한다면 각 확률이 0.8, 0.2, 0.4의 확률을 갖게 됨
  • 이를 전체 1로 맞춰 줄 수 있는 방법? → 소프트맥스 함수를 이용하는 것임

2. 소프트맥스 함수

1) 소프트맥스 함수의 이해

  • k차원 벡터 i번째 원소 zi, i번째 클래스 정답 확률 pi

k = 3, 벡터 z = [z1,z2,z3]
1-virginica 2-setosa 3-versicolor 셋 중 가장 높은 확률로 택.

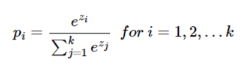
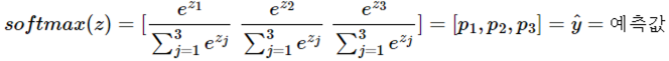
2) 그림을 통한 이해

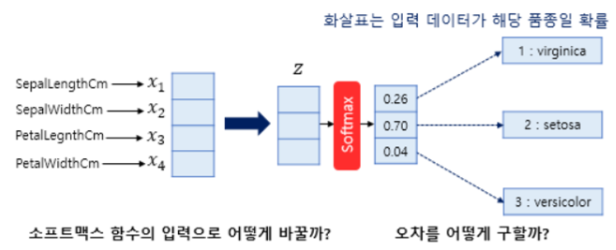
  • 소프트맥스 함수의 입력값으론 3차원 벡터로 받아줘야하는 데 현재 원래 샘플 데이터는 4개의 변수를 가진 4차원 벡터.

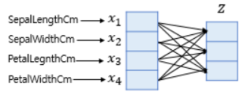
  • 소프트맥수 함수의 입력 벡터 z의 차원수만큼 결과가 나오도록 가중치곱.
  • 4*3 = 12개. 전부 다른 가중치. 이 오차들을 최소하는 가중치의 값으로 변경
  • 오차 계산 방법 : 일반적으로 소프트맥스 함수 출력은 클래스 개수만큼 차원 가지는 벡터 → 0과 1사이 값 가짐.
  • 여기서 나온 예측값과 실제값과의 차이를 보여줄 수 있는 것을 원-핫 벡터와 예측값의 차이로 표현.

 

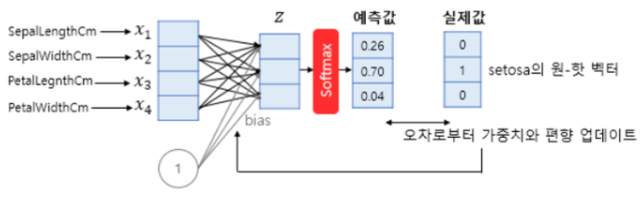
3. 원-핫 벡터의 무작위성

  • 다중 클래스 분류에서 각 클래스 간의 관계가 균등하다고 표시하기 위해 원-핫 벡터가 적절한 표현 법이라 할 수 있다.
  • {Banana :1, Tomato :2, Apple :3, Strawberry :4, ... Watermelon :10}
  • banana, tomato 거리는 1, banana, watermelon 거리는 81
  • 이는 각 클래스마다 차이가 있다는 것으로 이런 차이를 없애주기 위해 모든 클래스를 균등하게 재분배해주는 것. → 이를 원-핫 벡터를 이용.

4. 비용 함수

1) 크로스 엔트로피 함수

  • y = 실제값, k = 클래스 개수, yj = 실제값 원-핫 벡터의 j번째 인덱스, pj = j번째 클래스 확률

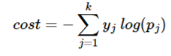
  • 비용 함수인 이유는 만약 c가 원-핫 벡터 1을 가진 원소 인덱스면
  • pc = 1 → yhat이 y를 제대로 예측. → cost = 0.
  • 이를 작게 해주는 방향으로 학습

2) 이진 분류에서 크로스 엔트로피 함수

  • 로지스틱 회귀의 크로스 엔트로피 함수식에서 소프트맥스 회귀 크로스 엔트로피 함수식 도출 가능.

저작자표시 변경금지